Лекция № 7- Правила преобразования алгоритмических схем

     Для анализа АСУ используются их алгоритмические схемы. Для упрощения (свертывания) сложных алгоритмических схем применяют правила их преобразования.

Три главных правила относятся к трем типовым соединениям элементов:

· последовательному;

· параллельному;

· встречно-параллельному (охват обратной связью).

Если эти соединения состоят из элементов направленного действия (с детектирующим свойством), то каждое такое соединение может быть заменено одним элементом, статические и динамические характеристики которого эквивалентны свойствам соединения.

Рассмотрим эти типовые соединения звеньев при известности их передаточных функций.

Последовательное соединение звеньев

Найдем передаточную функцию W(p) звена (рис.4.2, б), эквивалентного последовательному соединению звеньев (рис.4.2, а).

 

Рис. 4.2. Алгоритмические схемы последовательного соединения звеньев (а)

и эквивалентного ему звена (б)

 

Искомая передаточная функция эквивалентного звена

 (4.1)

 

Параллельное соединение звеньев

Найдем передаточную функцию W(p) звена (рис.4.3, б), эквивалентного параллельному соединению звеньев (рис.4.3, а).

 

Рис. 4.3. Алгоритмические схемы параллельного соединения звеньев (а)

и эквивалентного ему звена (б)

 

 

Искомая передаточная функция эквивалентного звена

 (4.2)

 

Встречно-параллельное соединение звеньев

Найдем передаточную функцию W(p) звена (рис.4.4, б), эквивалентного встречно-параллельному соединению звеньев (рис.4.4, а).

 

Рис. 4.4. Алгоритмические схемы встречно-параллельного соединения звеньев (а)

и эквивалентного ему звена (б)

 

Передаточная функция соединения

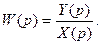 (4.3)

Но при этом

 (4.4)

Здесь W_П(p) и W_ОС (p) – передаточные функции соответственно прямой цепи и цепи обратной связи встречно-параллельного соединения звеньев.

После деления обеих частей равенства (4.4) на X(p) получаем

 (4.5)

Учитывая соотношение (4.3) в равенстве (4.5), последнее приводим к виду

 (4.6)

Решая уравнение (4.6) находим искомую передаточную функцию эквивалентного звена

 (4.7)

При отрицательной обратной связи передаточная функция эквивалентного звена

 (4.8)

 

При положительной обратной связи передаточная функция эквивалентного звена

 (4.9)

С помощью рассмотренных правил удается преобразовать (упростить) к простейшему виду (рис.4.4, б) любую алгоритмическую схему, не содержащую перекрестных связеймежду звеньями. Если же схема многоконтурная и содержит перекрестные связи, то эти правила можно применять лишь после устранения этих перекрестных связей. Для устранения перекрестных связей следует использовать ряд вспомогательных правил преобразований алгоритмических схем, которые приведены в табл. 4.1.

Таблица 4.1

 

№	Операция	Исходная схема	Преобразованная схема
	Перестановка узлов разветвления
	Перестановка сумматоров
	Перенос узла разветвления через звено вперед
	Перенос узла разветвления через звено назад
	Перенос сумматора через звено вперед
	Перенос сумматора через звено назад

 

Пример применения правил преобразования алгоритмических схем

Преобразовать алгоритмическую схему АСУ (рис. 4.5, а), содержащую звенья с известными передаточными функциями, к схеме с одним эквивалентным звеном.

В табл. 4.2 приведена: информация после каждой операции преобразования.

Таблица 4.2

Наименование операции преобразования	Передаточная функция эквивалентного звена	№ рисунка с преобразованной алгоритмической схемой
	Перенос сумматора В через звено 1 назад		4.5, б
	Перестановка сумматоров А и В		4.5, в
	Замена параллельного соединения звеньев 2 и 4		4.6, а
	Замена последовательного соединения звеньев 1 и 8		4.6, б
	Замена последовательного соединения звеньев 6 и 7		4.6, в
	Замена встречно-параллельного соединения звеньев 5 и 9		4.6, г
	Замена последовательного соединения звеньев 3 и 11		4.6, д
	Замена встречно-параллельного соединения звеньев 10 и 12		4.6, е

Рис. 4.5. Алгоритмические схемы АСУ

Рис. 4.6. Алгоритмические схемы АСУ

4.3. Передаточные функции типовой одноконтурной АСУ

Под типовой одноконтурной АСУ будем понимать систему, обобщенная функциональная схема которой приведена на рис. 1.6, в. Ей соответствует обобщенная алгоритмическая схема (рис. 4.7). Объект управления характеризуется одной управляемой переменной X(p), которую требуется стабилизировать на заданном уровне X_З(p). На стабилизируемую переменную X(p) влияет возмущение X_В(p). Отклонение стабилизируемой переменной X(p), вызываемое этим возмущением компенсируется в системе целенапрвленными изменениями управляющего воздействия Y(p), которое создается регулятором (управляющим устройством). На входе регулятора с передаточной функцией W_Р(p) действует сигнал рассогласования (ошибки) e(p). Этот сигнал формируется в результате сравнения (алгебраического суммирования) задающего воздействия X_З(p) и управляемой величины X(p),

 

Составим передаточные функции и уравнение динамики (движения) типовой одноконтурной АСУ, алгоритмическая схема которой приведена на рис. 4.7.

 

Рис. 4.7. Обобщенная алгоритмическая схема АСУ

Передаточная функция АСУ по задающему воздействию - передаточная функция преобразованной разомкнутой АСУ с одним звеном при возмущающем воздействии X_В(p) = 0 (рис. 4.8).

Она имеет вид

 (4.10)

 

 

 

Рис. 4.8. Алгоритмическая схема АСУ для определения ее передаточной функции

по задающему воздействию

Передаточная функция АСУ по возмущающему воздействию - передаточная функция преобразованной разомкнутой АСУ с одним звеном при задающем воздействии X_З(p) = 0 (рис. 4.9).

Она имеет вид

 (4.11)

 

 

 

Рис. 4.9. Алгоритмическая схема АСУ для определения ее передаточной функции

по возмущающему воздействию

 Согласно принципу наложения общее изменение выходной величины X(p), возникающее при совместном действии входных воздействий X_З(p) иX_В(p), равно сумме изменений, создаваемых каждым воздействием в отдельности. Отсюда уравнение динамики АСУ в краткой записи

 (4.12)

или в развернутом виде

 (4.13)

4.4. Типовые алгоритмы управления в линейных АСУ

Алгоритм управления (регулирования) в АСУ устанавливает связь ошибки e(p) и управляющего воздействия Y(p),

Эта связь в типовой одноконтурной АСУ (рис. 4.7) определяется передаточной функцией регулятора

 (4.14)

В линейных АСУ применяются следующие типовые алгоритмы управления (регулирования):

· пропорциональный (П) алгоритм;

· интегральный (И) алгоритм;

· пропорционально-интегральный (ПИ) алгоритм;

· пропорционально-дифференциальный (ПД) алгоритм;

· пропорционально-дифференциально-интегральный (ПИД) алгоритм;

Пропорциональный алгоритм регулирования (П-алгоритм).

Это простейший алгоритм, который реализуется при помощи безинерционного звена с передаточной функцией

 (4.15)

Так как управляющее воздействие пропорционально сигналу ошибки

 (4.16)

то и алгоритм получил название пропорционального, а регулятор – П-регулятора.

Преимущества П-регулятора – простота и быстродействие, недостатки – ограниченная точность (особенно при управлении объектами с большой инерционностью и запаздыванием).

Интегральный алгоритм регулирования (И-алгоритм).

Этот алгоритм реализуется при помощи интегрального звена с передаточной функцией

 (4.17)

 

Так как управляющее воздействие пропорционально интегралу сигнала ошибки

 (4.18)

то и алгоритм получил название интегрального, а регулятор И-регулятора.

При интегральном алгоритме регулирования управляющее воздействие y в каждый момент времени пропорционально интегралу от сигнала ошибки e. Поэтому И-регулятор реагирует главным образом на длительные отклонения управляемой величины x от заданного значения x_з.Кратковременные отклонения сглаживаются таким регулятором.

Преимущества И-регулятора – лучшая (по сравнению с П-регулятором) точность в установившихся режимах, недостатки – худшие свойства в переходных режимах (меньшее быстродействие и более высокая колебательность).

Пропорционально-интегральный алгоритм регулирования (ПИ-алгоритм).

Этот алгоритм реализуется при помощи регулятора с передаточной функцией

 (4.19)

Так как управляющее воздействие пропорционально как самому сигналу ошибки, так и его интегралу

 (4.20)

то алгоритм получил название пропорционально-интегрального, а регулятор – ПИ-регулятора.

Благодаря наличию интегральной составляющей в алгоритме, ПИ-регулятор обеспечивает высокую точность в установившихся режимах, а при определенном соотношении коэффициентов k_П и k_И обеспечивает хорошие показатели и в переходных режимах. Поэтому он получил наибольшее распространение в промышленной автоматике.

Пропорционально-дифференциальный алгоритм регулирования (ПД-алгоритм).

Этот алгоритм реализуется при помощи регулятора с передаточной функцией

 (4.21)

Так как управляющее воздействие пропорционально как самому сигналу ошибки, так и его производной

 (4.22)

то алгоритм получил название пропорционально-дифференциального, а регулятор – ПД-регулятора.

ПД-регулятор реагирует не только на величину сигнала ошибки, но и на скорость его изменения. Благодаря этому при регулировании достигается эффект упреждения. Недостатком ПД-регулятора является невозможность обеспечения высокой точности регулирования.

Пропорционально-интегрально-дифференциальный алгоритм регулирования (ПИД-алгоритм).

Этот алгоритм реализуется при помощи регулятора с передаточной функцией

 (4.23)

Так как управляющее воздействие пропорционально как самому сигналу ошибки, так и его интегралу и производной

 (4.24)

то алгоритм получил название пропорционально-интегрально-дифференциального, а регулятор – ПИД-регулятора.

ПИД-алгоритм – наиболее гибкий алгоритм регулирования (в классе линейных алгоритмов). Он сочетает в себе преимущества более простых выше рассмотренных алгоритмов.

Коэффициенты k_П, k_И, k_Д, входящие в передаточные функции типовых регуляторов, подлежат настройке при наладке АСУ и поэтому называются настроечными параметрами. Они имеют наименования: k_П, k_И, k_Д - коэффициенты пропорциональной, интегральной и дифференциальной частей АСУ.

4.5. Методы моделирования АСУ на ЦВМ

Мощным инструментом при решении задач ТАУ являются цифровые вычислительные машины (ЦВМ), в частности персональные электронные вычислительные машины (ПЭВМ).

Целью моделирования АСУ на ЦВМ является расчет изменения управляемой величины x(t) в переходном режиме. Результаты этого расчета необходимы при анализе работы АСУ и ее создании (синтезе).

Моделирование АСУ на ЦВМ в зависимости от применяемых математических методов можно осуществлять двумя путями:

· путем численного интегрирования;

· путем структурного моделирования.

Численное интегрирование – интегрирование совокупности дифференциальных уравнений, описывающих движение (изменение режимных параметров во времени) АСУ.

Весьма удобным инструментом для осуществления численного интегрирования является программный продукт «VisSim» для ПЭВМ, предназначенный преимущественно для моделирования виртуальных устройств, входящих в состав АСУ.

Из виртуальных устройств, имеющихся в продукте «VisSim», можно собирать алгоритмические схемы для решения системы дифференциальных и/или алгебраических уравнений и отображать результаты решения на различных виртуальных индикаторах (стрелочных показывающих приборах, дисплее, графопостроителе и т. п.).

Для численного интегрирования системы дифференциальных уравнений, описывающих переходный процесс в АСУ, эти уравнения следует представлять в нормальной форме Коши, т. е. разрешенными относительно первых производных.

Структурное моделирование – моделирование осуществляемое с помощью алгоритмической схемы АСУ, состоящей из типовых динамических звеньев, арифметических звеньев и/или звеньев с известными передаточными функциями.

Весьма удобным инструментом для реализации структурного моделирования также является программный продукт «VisSim». В нем преимущественно с помощью блоков «Transfer function» собирается алгоритмическая схема АСУ, которая и используется для анализа работы системы.

Пример моделирования АСУ путем численного интегрирования на ЦВМ

Для автоматической системы стабилизации напряжения на выходе r-c фильтра низкой частоты, нагруженного на резистор с сопротивлением r_н, включающей П-регулятор Р (коэффициент пропорциональности k_П) и компаратор К, схема электрическая принципиальная которой приведена на рис. 4.10, составим алгоритмическую схему для численного интегрирования на ПЭВМ.

 

 

 

Рис.4.10. Схема электрическая принципиальная АСУ

Система уравнений движения АСУ имеет вид

 (4.25)

После исключения ряда параметров и приведения к виду Коши эта система уравнений принимает вид

 (4.26)

 

Используя полученную систему уравнений, составляем искомую алгоритмическую схему АСУ для ее моделирования путем численного интегрирования на ПЭВМ с использованием программного пакета «VisSim» (рис. 4.11).

 

Рис. 4.11. Алгоритмическая схема АСУ для ее моделирования путем численного интегрирования на ПЭВМ с использованием программного пакета «VisSim»

Пример структурного моделирования АСУ на ЦВМ

Для автоматической системы стабилизации напряжения на выходе r-c фильтра низкой частоты, нагруженного на резистор с сопротивлением r_н, включающей П-регулятор Р (коэффициент пропорциональности k_П) и компаратор К, схема электрическая принципиальная которой приведена на рис. 4.10, составим алгоритмическую схему для структурного моделирования на ПЭВМ.

Применим к системе уравнений движения АСУ (4.26) прямое интегральное преобразование Лапласа при нулевых начальных условиях и получим

 (4.27)

После проведения алгебраических преобразований первого уравнения системы (4.27) приводим ее к виду

 (4.28)

Введем обозначения:

 - передаточная функция фильтра (объекта управления). (4.29)

 - передаточная функция регулятора (4.30)

Учитывая эти обозначения в системе (4.28) приводим ее к виду

 (4.31)

Используя полученную систему уравнений, составляем искомую алгоритмическую схему АСУ для ее структурного моделирования на ПЭВМ с использованием программного пакета «VisSim» (рис. 4.12).

 

 

 

Рис. 4.12. Алгоритмическая схема АСУ для ее структурного моделирования на ПЭВМ с использованием программного пакета «VisSim»

5. АНАЛИЗ УСТОЙЧИВОСТИ ЛИНЕЙНЫХ АСУ

Вы узнаете:

· Что такое устойчивость АСУ.

· Общее математическое условие устойчивости.

· Какие критерии применяют при анализе устойчивости АСУ.

· Что такое области устойчивости АСУ и как их определяют.

· Как влияют структура и параметры АСУ на ее устойчивость.

5.1. Что такое устойчивость АСУ?

Одной из важнейших характеристик АСУ является ее устойчивость.

Устойчивость АСУ – свойство системы возвращаться в состояние равновесия после прекращения изменения воздействия, выведшего систему из этого состояния.

Неустойчивая АСУ не возвращается в состояние равновесия, а непрерывно удаляется от него

От устойчивости АСУ зависит ее работоспособность. Система, не обладающая устойчивостью, вообще не способна выполнять функции управления и имеет нулевую или даже отрицательную эффективность. Неустойчивая система может привести управляемый объект в аварийное состояние. Поэтому проблема устойчивости систем является одной из центральных в теории автоматического управления.

Проявлением, по которому можно судить об устойчивости или неустойчивости системы, является характер изменения ее сигналов во времени, например, управляемой величины x(t). Если управляемая величина x(t) после прекращения изменения, например, задающего воздействия x_з(t)становитя с течением времени постоянной (рис.5.1, а), то система ведет себя устойчиво. Если же управляемая величина x(t) – возрастает, то система ведет себя неустойчиво.

Рис. 5.1. Графики изменения сигналов АСУ во времени

а – устойчивая АСУ; б – неустойчивая АСУ

Вскроем причины неустойчивости АСУ.

Неустойчивость АСУ возникает, как правило, из-за неправильного (положительного) или очень сильного действия главной обратной связи. В результате чего в систему в режиме гармонических колебаний непрерывно поступает (закачивается) энергия. Энергия системы увеличивается. Увеличиваются и связанные с ней режимные параметры, например, регулируемая величина. Такое явление в технике получило название резонанса.

Причинами неправильного действия главной обратной связи АСУ являются:

· Выполнение главной обратной связи АСУ по ошибке положительной вместо отрицательной, что практически при любых параметрах делает систему неустойчивой.

· Значительная инерционность элементов замкнутого контура АСУ (например, объекта управления), из-за которой в режиме колебаний системы сигнал главной обратной связи (например, управляемая величина) значительно отстает от входного сигнала (например, управляющего воздействия) и оказывается с ним в фазе. Это означает, что связь, выполненная конструктивно как отрицательная, в динамическом режиме (режиме гармонических колебаний) начинает на определенной частоте действовать как положительная. Это ведет к раскачиванию системы и нарушению ее устойчивости.

Задачами анализа устойчивости АСУ обычно являются:

· определение устойчивости или неустойчивости системы при заданных параметрах;

· определение допустимого по условиям устойчивости диапазона изменения некоторых незаданных параметров системы;

· выяснение принципиальной возможности устойчивости системы при заданной ее структуре.

5.2. Общее математическое условие устойчивости

Согласно данному выше физическому определению устойчивость определяется характером движения системы, когда воздействия, выведшие ее из состояния равновесия, прекратили действовать или изменяться во времени. Такое движение системы называют свободным. Оно происходит за счет внутренней энергии самой системы и зависит только от ее свойств (параметров).

Свободное движение линейной или линеаризованной АСУ описывается однородным дифференциальным уравнением

 (5.1)

где x(t) – свободная составляющая выходной (управляемой) величины системы.

Вынужденная составляющая выходной величины, зависящая от вида внешнего воздействия и соответственно от правой части уравнения (2.19) на устойчивость системы не влияет.

С математической точки зрения:

· системаустойчива, если свободная составляющая x(t) переходного процесса с течением времени стремится к нулю;

· системанеустойчива, если свободная составляющая x(t) переходного процесса с течением времени неограниченно возрастает;

· система находится на границе устойчивости, если свободная составляющая x(t) переходного процесса с течением времени не стремится ни к нулю, ни к бесконечности.

Решение уравнения (5.1) равно сумме

 (5.2)

где C_k – постоянные, зависящие от начальных условий; p_k – корни характеристического уравнения

 (5.3)

Корни характеристического уравнения могут быть действительными (p_k = a_k), мнимыми (p_k = jb_k) и комплексными (p_k = a_k ± jb_k). При этом комплексные корни всегда попарно сопряжены между собой: если есть корень с положительной мнимой частью, то обязательно существует корень с такой же по модулю, но отрицательной мнимой частью.

 

Переходная составляющая (5.2) при времени t ® ¥ стремится к нулю лишь в том случае, если каждое слагаемое вида Характер этой функции времени зависит от вида корня p_k . На рис.5.1 изображены возможные случаи расположения корней p_k на комплексной плоскости и соответствующие им функции x_k(t), которые показаны внутри окружностей.

 

Рис. 5.1. Влияние корней характеристического уравнения АСУ на составляющие ее свободного движения

Анализ рис.5.1 позволяет сформулировать общее математическое условие устойчивости: для устойчивости линейной АСУ необходимо и достаточно, чтобы действительные части всех корней характеристического уравнения системы были отрицательными (или чтобы все корни характеристического уравнения системы располагались в левой части комплексной плоскости).

Устойчивость системы зависит только от вида корней характеристического уравнения и не зависит от характера внешних воздействий на систему, т. е. устойчивость есть внутреннее свойство системы, присущее ей вне зависимости от внешних условий.

Если хотя бы один корень имеет положительную действительную часть (располагается в правой части комплескной плоскости), то система будет неустойчивой.

Мнимая ось jb является границей устойчивости в плоскости корней. Если характеристическое уравнение имеет пару чисто мнимых корней (p_k= +jb_k , p_k+1 =- jb_k), а все остальные корни находятся в левой части комплексной плоскости, то в системе устанавливаются незатухающие гармонические колебания с круговой частотой w = | b_k | . В этом случае говорят, что система находится на колебательной границе устойчивости.

Если характеристическое уравнение имеет нулевой корень (b = 0), то система находится на апериодической границе устойчивости. Если таких корня два, то система неустойчива.

Применяя сформулированное выше условие для оценки устойчивости реальных АСУ, не следует забывать, что линейные уравнения вида (5.1), как правило , получаются в результате упрощений и линеаризации исходных нелинейных уравнений. Возникает вопрос: в какой мере оценка устойчивости по линеаризованному уравнению будет справедлива для реальной системы, и не окажут ли существенное влияние на результат анализа отброшенные при линеаризации члены разложения? Ответ на него был дан русским математиком А. М. Ляпуновым в 1892 г. в работе «Общая задача об устойчивости движения». Он сформулировал и доказал следующую теорему: если характеристическое уравнение линеаризованной системы имеет хотя бы один нулевой корень или одну пару мнимых корней, то судить об устойчивости реальной системы по линеаризованному уравнению нельзя. Отброшенные при линеаризации малые члены могут сделать систему неустойчивой, и поэтому устойчивость реальной системы необходимо оценивать по исходному нелинейному уравнению.

Характеристическое уравнение АСУ можно составлять не только по дифференциальному уравнению (5.1) ее свободного движения, но и по ее алгоритмической схеме с известными передаточными функциями звеньев.

Получим характеристическое уравнение разомкнутой АСУ, алгоритмическая схема которой приведена на рис.5.2, а.

Ее уравнение движения

, (5.4)

или представляя передаточную функцию системы в виде

 (5.5)

где K(p) и D(p) – входной и собственный операторы, уравнение движения приводим к виду

 (5.6)

Полагая в уравнении (5.6) задающее воздействие X_З(p) = 0 записываем уравнение свободного движения АСУ

 (5.7)

Откуда искомое характеристическое уравнение разомкнутой АСУ

 

 (5.8)

 

Рис.5.2. Алгоритмические схемы АСУ

а – разомкнутой; б – типовой замкнутой

Получим характеристическое уравнение типовой замкнутой АСУ, алгоритмическая схема которой приведена на рис.5.2, б.

Ее уравнение движения

 (5.9)

или с учетом обозначения (5.5)

 (5.10)

Полагая в уравнении (5.10) X_З(p) = 0, записываем уравнение свободного движения АСУ

 (5.11)

Тогда искомое характеристическое уравнение типовой замкнутой АСУ

 (5.12)