Комплексным числом называется число вида
z= x+ i y ,
где x и y действительные числа,
а i – мнимая единица такая, что
 .
.
При этом такая запись комплексного числа называется алгебраической
x=Re(z) - называется действительной частью комплексного числа
y=Im(z) - называется мнимой частью комплексного числа
Каждое комплексное число может быть так же представлено в тригонометрической форме
или показательной форме:
где
– модуль комплексного числа,
а
– аргумент комплексного числа такой, что
, где
или
.
Вывод:
Для любого ненулевого комплексного числа
Для любого ненулевого комплексного числа
Для любого ненулевого комплексного числа существует ровно n корней n-й степени из комплексного числа z
где ,– арифметический кореньn-й степени из положительного числа
Для любого ненулевого комплексного числа существует ровно n корней n-й степени из комплексного числа z все они могут быть найдены по формуле
Формы комплексного числа |
|||
|
алгебраическая |
|
x=Re(z) |
действительная часть комплексного числа |
|
y=Im(z)
|
мнимая часть комплексного числа |
||
|
|
|
модуль комплексного числа |
|
|
|
аргумент комплексного числа |
||
|
|
или |
||
| показательная | |
||
| тригонометрическая | |
||
| Формула Эйлера | cos φ + i sin φ = e iφ | ||
|
Формула Муавра |
|
||
| Корни из комплексных чисел | |||
| Для любого ненулевого комплексного числа существует ровно n корней n-й степени из комплексного числа z все они могут быть найдены по формуле | |
||
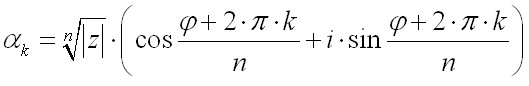 |
где
|
||
Комплексные числа изображаются на комплексной плоскости.

Для них введены операции сложения, умножения, вычитания и деления. Так же их можно возводить в степень и извлекать из них корень, для этого используют формулу Муавра.
Примеры
| Задание | Представить в показательной и тригонометрической формах комплексное число |
| Решение | Найдем модуль заданного комплексного числа, по условию действительная часть Вычислим аргумент заданного комплексного числа: Тогда тригонометрическая форма этого комплексного числа будет иметь вид: показательная: |
| Ответ | 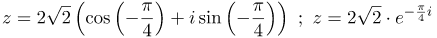 |





Поделиться с друзьями: